Simple geometry question
You have 9 points arranged in a 3x3 grid, as show in the photo. Can you cross all of them with 4 lines, without lifting your pen from the paper?

Acute Triangles
If I have an obtuse-angled triangle, can it be divided into only acute-angled triangles?
Reminder: Right angles are not acute
Reminder: Right angles are not acute
How Many Children?
You came to visit a friend and saw children playing in the back yard. You were curious whether all the children were his.
-"Of course not. My family is the biggest, but there are kids from 3 other families playing there: The Whites have smaller number of children, the Browns have a still smaller number, and the Blacks the smallest.".
-"How many children overall?" you insist, this is too complicated.
-"There are less than 18 children, and the product of all the numbers is my house number". Aha! You almost know the answer now, you just ask one last question: "Is there more than one child in the black family?". When your friend replies -- you know the answer.
How many children in each family?
-"Of course not. My family is the biggest, but there are kids from 3 other families playing there: The Whites have smaller number of children, the Browns have a still smaller number, and the Blacks the smallest.".
-"How many children overall?" you insist, this is too complicated.
-"There are less than 18 children, and the product of all the numbers is my house number". Aha! You almost know the answer now, you just ask one last question: "Is there more than one child in the black family?". When your friend replies -- you know the answer.
How many children in each family?
Transparent Rabbit
There are 10 cells in a line. A transparent rabbit is in one of them. You have a paintball gun and you win when you can see (and catch) the rabbit.
If you hit a cell with the rabbit -- the rabbit is visible and you win. If you hit an empty cell, the rabbit hears the shot and jumps to and adjacent cell on either side (i.e., when it's in the corner it'll jump to the available adjacent cell).
Can you capture the rabbit?
If you hit a cell with the rabbit -- the rabbit is visible and you win. If you hit an empty cell, the rabbit hears the shot and jumps to and adjacent cell on either side (i.e., when it's in the corner it'll jump to the available adjacent cell).
Can you capture the rabbit?
The Flight Club
You are a member of a prestigious flight club based on a secret remote island. To show just how exciting your flying club is, you plan a flight around the world! What makes this flight challenging is that the fuel tanks of your airplanes have enough fuel for only half the trip. What is the minimum number of members you need in your club to successfully complete this trip?
The expected rules apply:
You cannot refuel anywhere except on your secret hidden island base.
You have the tech to do 0-time air refueling (from plane to plane)
The expected rules apply:
You cannot refuel anywhere except on your secret hidden island base.
You have the tech to do 0-time air refueling (from plane to plane)
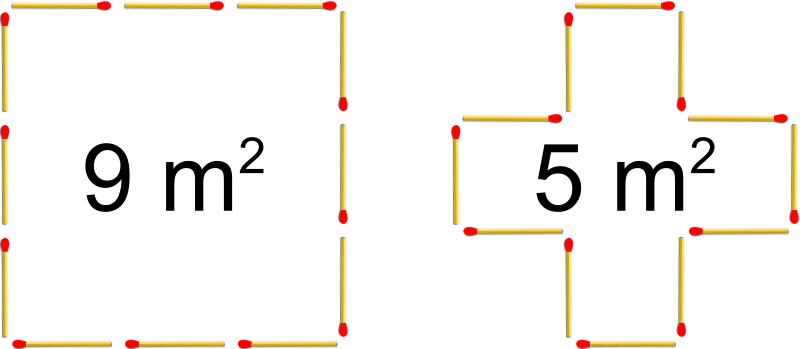
12 Matches
There are many shapes that can be constructed from 12 matches.
If our unit of length is 1 match, in the image I show 2 such shapes: One with area of 9 square matches, and one with area of 5 square matches.
Can you build a shape with 12 match perimeter and area of 4 square matches?
Reasonable rules apply: it has to be a perimeter, and full lengths of matches must be used.
If our unit of length is 1 match, in the image I show 2 such shapes: One with area of 9 square matches, and one with area of 5 square matches.
Can you build a shape with 12 match perimeter and area of 4 square matches?
Reasonable rules apply: it has to be a perimeter, and full lengths of matches must be used.
The Commuter
A daily commuter always returned home on the same train, arriving the station at exactly 5pm. His neighbor always arrived the station at 5pm to pick him up.
One day he had an offsite that finished early so he got on an earlier train, that arrived to the station at 4pm. His phone was dead, so he started walking on the route that his neighbor takes to meet him somewhere along the way.
They met and arrived home 10min before the usual time.
Assuming physical car and driving conditions (i.e., the same operation takes the same time). How long did the commuter walk?
One day he had an offsite that finished early so he got on an earlier train, that arrived to the station at 4pm. His phone was dead, so he started walking on the route that his neighbor takes to meet him somewhere along the way.
They met and arrived home 10min before the usual time.
Assuming physical car and driving conditions (i.e., the same operation takes the same time). How long did the commuter walk?
 Normal Birds
Normal Birds
Lets use the term /normal/ for a bird that is fond of at least one bird. Q7 (https://www.facebook.com/groups/mockamockingbird/permalink/168283056892135/) asked you to prove that every normal bird is happy (the reverse is not necessarily true).
Prove that if composition C1 holds, and if there is at least one happy bird in the forest then there is at least one normal bird.
Prove that if composition C1 holds, and if there is at least one happy bird in the forest then there is at least one normal bird.
Inaccurate Liars 2
Lets continue with the 4 brothers we met last time: A(rthur), B(ernard), C(harles), D(avid). Where A is an accurate truth-teller, B is an inaccurate truth-teller (all is beliefs are incorrect, but he never lies about it), C is an accurate liar and D is an inaccurate liar (he's both delusional and dishonest).
Q6: https://www.facebook.com/groups/mockamockingbird/permalink/157621477958293/
This is a preparation for the next puzzle:
Lets discuss a basic principal about accurate and inaccurate truth-tellers and liars. If you ask the 4 brothers whether 2+2=4, A & D will say Yes, and B & C will answer No.
What if I ask "Do you believe that 2+2 equals 4?"
What will each brother answer?
Q6: https://www.facebook.com/groups/mockamockingbird/permalink/157621477958293/
This is a preparation for the next puzzle:
Lets discuss a basic principal about accurate and inaccurate truth-tellers and liars. If you ask the 4 brothers whether 2+2=4, A & D will say Yes, and B & C will answer No.
What if I ask "Do you believe that 2+2 equals 4?"
What will each brother answer?
Chessboard with missing cells
Since no one answered my previous questions about the inaccurate truth tellers and liars, I'l try something new:
Imagine that you have a chessboard (a black and white 8x8 board) and a set of 32 domino pieces. It's easy to see how the 32 dominos can cover the whole chessboard.
Now imagine that I broke off 2 squares from the diagonals of the chessboard (as in the attached illustration). Can I fully cover it with 31 dominos?
Imagine that you have a chessboard (a black and white 8x8 board) and a set of 32 domino pieces. It's easy to see how the 32 dominos can cover the whole chessboard.
Now imagine that I broke off 2 squares from the diagonals of the chessboard (as in the attached illustration). Can I fully cover it with 31 dominos?

 Compatible Birds
Compatible Birds
Two birds A and B are called /compatible/ if there is a bird x and a bird y (same or different) such that:
Ax = y
By = x
Prove that if conditions C1 (composition) and C2 (Mockingbird) hold, then any two birds are compatible
Ax = y
By = x
Prove that if conditions C1 (composition) and C2 (Mockingbird) hold, then any two birds are compatible
The Inaccurate Liars
We had our liars and truth tellers, but now we have inaccurate truth tellers and inaccurate liars!
Example:
If we ask whether 2+2 equal 4
The liar will say No, the truth teller will say Yes, and inaccurate liar will say Yes! because he believes that 2+2 does not equal 4, so he'll lie and say that the answer is yes.
We have 4 brothers: A(rthur), B(ernard), C(harles), D(avid). The 4 are identical in any way except that A is an accurate truth-teller, B is an inaccurate truth-teller (all is beliefs are incorrect, but he never lies about it), C is an accurate liar and D is an inaccurate liar (he's both delusional and dishonest).
a. You meet one of the brothers and wish to know his first name. Find the fewest number of questions to do it (and tell me the questions)
b. A and B are both married, the other two are not. A and C are both rich, the other two are not. You meet one of the brothers and wish to find out whether he's married. What *short* yes/no question can you ask?
c. Now you want to find out whether he is rich. What should you ask?
d. I once met one of the four brothers and asked a yes/no question, I should have realized that it was pointless since I could have known in advance what the answer would be. What did I ask?
Example:
If we ask whether 2+2 equal 4
The liar will say No, the truth teller will say Yes, and inaccurate liar will say Yes! because he believes that 2+2 does not equal 4, so he'll lie and say that the answer is yes.
We have 4 brothers: A(rthur), B(ernard), C(harles), D(avid). The 4 are identical in any way except that A is an accurate truth-teller, B is an inaccurate truth-teller (all is beliefs are incorrect, but he never lies about it), C is an accurate liar and D is an inaccurate liar (he's both delusional and dishonest).
a. You meet one of the brothers and wish to know his first name. Find the fewest number of questions to do it (and tell me the questions)
b. A and B are both married, the other two are not. A and C are both rich, the other two are not. You meet one of the brothers and wish to find out whether he's married. What *short* yes/no question can you ask?
c. Now you want to find out whether he is rich. What should you ask?
d. I once met one of the four brothers and asked a yes/no question, I should have realized that it was pointless since I could have known in advance what the answer would be. What did I ask?
 Composition Exercise
Composition Exercise
Suppose that condition C1 (composition) holds, prove that for any birds A, B and C there is a bird D such that for every bird x:
Dx = A(B(Cx))
This fact is useful
[Check the pinned post for quick reference to instructions & past questions]
Dx = A(B(Cx))
This fact is useful
[Check the pinned post for quick reference to instructions & past questions]
Twin Sisters
A certain logician, though absolutely brilliant in theoretical matters was extremely unobservant and highly absent minded. He met 2 beautiful twin sisters named T(eresa) and L(enora). T always told the truth and L always lied. He married one of them, but forgot to find out her first name!
a. The logician met one of the two sisters at a logic conference, and wanted to know whether she's his wife. What short yes/no question can he ask?
b. A few days later, he again met one of them, and this time wanted to know the first name of his wife. What short yes/no question can he ask?
c. What if the logician wanted to know both pieces of information, the identity of the sister he met and the name of his wife. Can he ask a better question?
a. The logician met one of the two sisters at a logic conference, and wanted to know whether she's his wife. What short yes/no question can he ask?
b. A few days later, he again met one of them, and this time wanted to know the first name of his wife. What short yes/no question can he ask?
c. What if the logician wanted to know both pieces of information, the identity of the sister he met and the name of his wife. Can he ask a better question?
3 Identical Brothers
We meet three identical brothers named John, James and William.
John and James always lie, but William always tells the truth. You meet one of them, and wish to find out whether he is John.
What one Yes/No question should you ask?
(Since I got complaints that the questions are too easy, I'll try having multi-section questions, and it's the weekend)
4.b:
Now I'm telling you that John and James are both telling the truth and William is a liar. You again meet one of them, and wish to know whether he's John. What Yes/No question should you ask?
John and James always lie, but William always tells the truth. You meet one of them, and wish to find out whether he is John.
What one Yes/No question should you ask?
(Since I got complaints that the questions are too easy, I'll try having multi-section questions, and it's the weekend)
4.b:
Now I'm telling you that John and James are both telling the truth and William is a liar. You again meet one of them, and wish to know whether he's John. What Yes/No question should you ask?
 Composition & Agreeable
Composition & Agreeable
Suppose that the composition condition C1 holds, and that A, B and C are birds such that C composes A with B.
Prove that if C is agreeable then A is also agreeable
[Check the pinned post for quick reference to past questions]
Prove that if C is agreeable then A is also agreeable
[Check the pinned post for quick reference to past questions]
4 Prizes
Suppose that it's the same as previous question (https://www.facebook.com/groups/mockamockingbird/permalink/146480429072398/) but I also add a fourth prize: D, this is also a fake prize. The conditions are the same: If you make a true statement, you'll get either prize A or prize B, if you make a false statement you'll get one of C or D.
For an unknown reason, you want prize C! Can you force me to give you prize C?
For an unknown reason, you want prize C! Can you force me to give you prize C?
 Agreeable birds
Agreeable birds
Two birds A and B are said to /agree/ on x if their responses are the same: Ax = Bx
A bird A is called /agreeable/ if for every bird B there is at least one bird x on which A and B agree, or in other words: Ax = Bx
Here's a variant of problem 1:
We're given the composition condition (C1), but not that there's a mockingbird, instead we know that there is an agreeable bird A
Is it enough to guarantee that every bird is fond of at least one bird?
A bird A is called /agreeable/ if for every bird B there is at least one bird x on which A and B agree, or in other words: Ax = Bx
Here's a variant of problem 1:
We're given the composition condition (C1), but not that there's a mockingbird, instead we know that there is an agreeable bird A
Is it enough to guarantee that every bird is fond of at least one bird?
3 Prizes
Suppose I offer you one of 3 prizes: prize A, prize B or prize C. Prize A is the best of the three, prize B is ok-ish and prize C is just something fake that's not even a prize.
You are to make a statement; if the statement is true I'll give you prize A or B, if your statement is false you'll get prize C (which is sad).
Can you force me to give you the good prize, prize A?
You are to make a statement; if the statement is true I'll give you prize A or B, if your statement is false you'll get prize C (which is sad).
Can you force me to give you the good prize, prize A?
 Egocentric Birds
Egocentric Birds
A bird x is called /egocentric/ if it is fond of itself: x's response to x is x.
x is egocentric iff xx = x
Prove that under conditions C1 and C2 (composition and Mockingbird, from the intro) at least one bird is egocentric
x is egocentric iff xx = x
Prove that under conditions C1 and C2 (composition and Mockingbird, from the intro) at least one bird is egocentric
3-color Flower Garden
In a certain flower garden, each flower was either (R)ed, (Y)ellow or (B)lue, and all three colors were represented. A statistician once visited the garden and made the observation that whatever three flowers you picked, at least one of them was bound to be (R)ed. A second statistician visited the garden and made the observation that whatever three flowers you picked, at least one was bound to be (Y)ellow.
Two logic students heard about this and got into an argument:
A: "it therefore follows that whatever three flowers you pick, at least one is bound to be (B)lue"
B: "Of course not!"
Which student is right, why?
Two logic students heard about this and got into an argument:
A: "it therefore follows that whatever three flowers you pick, at least one is bound to be (B)lue"
B: "Of course not!"
Which student is right, why?
 Birds!
Birds!
We say that bird A is /fond/ of bird B if the response of A to B is B:
AB = B
In normal math terms: B is a fixed point of A
The forest satisfies the following 2 conditions:
1) C1: the composition condition
2) Mockingbird M exists
Prove that every bird in the forest is fond of at least one bird
AB = B
In normal math terms: B is a fixed point of A
The forest satisfies the following 2 conditions:
1) C1: the composition condition
2) Mockingbird M exists
Prove that every bird in the forest is fond of at least one bird
Intro
This is a group for puzzles, hints and solutions (but hidden, without spoilers).
A certain enchanted forest is inhabited by talking birds. Given any birds A and B, if you call out the name of B to A, then A will respond by calling out the name of some bird to you; this bird we designate AB. Thus AB is the bird named by A upon hearing the name of B.
C1: Composition: Given any birds A, B & C the bird C is said to compose A with B if for every bird x the following condition holds:
A(Bx) = Cx
C2: Mockingbird: a bird M such that for any bird x, the following condition holds:
Mx = xx
M is called a mockingbird for the simple reason that its response to any bird x is the same as x's response to itself -- in other words, M mimics x as far as its response to x goes.
A certain enchanted forest is inhabited by talking birds. Given any birds A and B, if you call out the name of B to A, then A will respond by calling out the name of some bird to you; this bird we designate AB. Thus AB is the bird named by A upon hearing the name of B.
C1: Composition: Given any birds A, B & C the bird C is said to compose A with B if for every bird x the following condition holds:
A(Bx) = Cx
C2: Mockingbird: a bird M such that for any bird x, the following condition holds:
Mx = xx
M is called a mockingbird for the simple reason that its response to any bird x is the same as x's response to itself -- in other words, M mimics x as far as its response to x goes.